Pluto Orbiter
How Gravity Assists can help us get into a Plutonian Orbit.
Extension and Results
As previously stated, New Horizons left Earth with an excess velocity of about 16 km/s, which was increased to 21 km/s after a Jupiter gravity assist. These will be used as the initial conditions for this analysis. As in, most of the analysis centers around leaving Jupiter with that velocity, and using other planets as a form of reducing velocity. Several assumptions are made here, namely, the planets are in circular orbits around the sun, with a radius of their semi-major axis. Another large assumption is that the planets will be aligned in such a way that they will be in the appropriate position as the spacecraft passes their orbit to actually perform a gravity assist. In reality, there are only moments every hundreds of years where this could be the case. While this is a large assumption, it gives us an understanding of how gravity assists can be used if the opportunity to transfer from planet to planet is possible.
The first portion of this analysis analyzes why this is necessary, simply put why was New Horizons not able to orbit Pluto. As stated earlier, New Horizons approached Pluto at approximately 14.5 km/s with respect to the sun. This translates to a hyperbolic excess velocity of 9.76 km/s. Using Equation (6) the Delta V needed at Pluto was 6.90 km/s. This is more than the on board systems would have been able to produce. The mission was very fast on its approach to Pluto however, taking under 10 years to do it. The image on the right shows New Horizons Heliocentric velocity as a function of its distance from the sun. The gravity assist as Jupiter can be seen, increasing the velocity of the spacecraft enough to escape the Solar System. Pluto's heliocentric velocity is shown as a reference. To decrease the needed Delta V at arrival, a spacecrafts heliocentric velocity will want to be as close to this value as possible.

Figure 4: New Horizons Speed through the Solar System.
Hohmann Transfer From Earth and Beyond
The first situation analyzed was a simple Hohmann transfer from Earth. This will give a baseline estimate of a minimal amount of Delta V that could be used during the transfer. This transfer assumes the spacecraft will leave Earth at a parking orbit of 185 km and perform two tangential burns on the way to Pluto. One as it leaves Earth's orbit on a hyperbolic trajectory out of the sphere of influence of Earth. This will put the spacecraft on a heliocentric elliptical orbit to Pluto, however it will not have enough velocity to escape the Solar System. The second burn occurs at Pluto's orbit, and will slow the spacecraft to have the same orbit about the sun as Pluto does. In this scenario, Pluto needs to be at the correct location in its orbit for the transfer to work.
The plot to the right shows the Hohmann transfer from Earth to Pluto, as well as a Hohmann transfer from both Saturn and Neptune to Pluto. These will be discussed below. As can be seen, the Hohmann transfer from Earth has the smallest semi-major axis, and therefore will take the shortest transfer time of these three trajectories. In fact, the transfer time from this low Earth orbit to Pluto is 45.67 years. That is longer than Voyager 2 has been on its mission and more than 4 times the length of New Horizons. This trajectory does have its advantages though, as the Delta V needed as the spacecraft approaches Pluto decreases to 3.68 km/s, almost half as much as New Horizons. For a better understanding of how saving Delta V helps, the Ideal Rocket Equation is shown below:
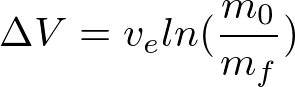
(8)
Although this equation makes quite a few assumptions, it shows that as the Delta V increases, the ratio of the initial and final mass also increases. Decreasing the Delta V by half changes the mass ration by a factor of e^(1/2), drastically decreasing the needed on board fuel. This is something to keep in mind throughout the analysis. So how can we decrease the velocity even more?
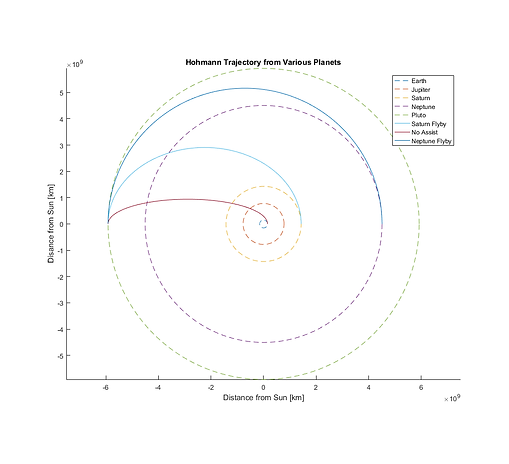
Figure 5: Hohmann transfers from different planets to Pluto
Saturn Flyby
The next situation analyzed was New Horizons trajectory from Earth to Jupiter, then using its velocity after the Jupiter flyby, the trajectory to Saturn was calculated, once at Saturn, the spacecraft performs a leading side flyby, decreasing its heliocentric velocity. Based on the radius of the flyby, a variety of outbound velocities can be obtained. The first outbound velocity tested was a velocity that would put the spacecraft on a Hohmann transfer to Pluto. This is not the fasted route, but will save fuel on the back end, as Hohmann transfers are a type of minimal energy transfers. In reality, many different velocities can be achieved after the flyby, either faster or slower that the inbound velocity. The outbound velocity will effect the transfer time from the planet the maneuver is based, and also the inbound velocity to the target. The Hohmann velocity was chosen because it will minimize the Delta V needed at Pluto.

The plot to the right shows the spacecraft's Heliocentric velocity with respect to distance. The Jupiter gravity assist is in the same location, increasing the velocity to 21 km/s. The Saturn gravity assist can also be seen. This gravity assist does its job in reducing the heliocentric velocity of the spacecraft. The velocity needed to be on a Hohmann transfer to Pluto from Saturn is 12.23 km/s. To achieve this velocity, the spacecraft flies by Saturn at a distance of 22640 km in front of the planet. This turns the spacecraft by 88.4 degrees. The maneuver decreases the satellites velocity by 4.68 km/s. This keeps the spacecraft in the Solar System and decreases its arrival velocity at Pluto to 2.95 km/s. Once on this trajectory, the spacecraft is now on an ellipse with a semi major axis equal to the mean of the distance from Saturn and Pluto to the sun. This axis is larger than the Hohmann transfer from Earth to Pluto, so this transfer will take more time. The total time of the transfer, from Earth to Jupiter, Jupiter to Saturn, and Saturn to Pluto takes 63 years. This is an incredible amount of time so hopefully it would pay off on the back end. The final Delta V that is needed to orbit Pluto is 1.26 km/s. This is a much more achievable Delta V although the time this transfer takes is very costly. The flyby was created in STK, for a visual representation of the scenario and can be seen below.
Figure 6: Spacecraft's velocity through the Solar System with a Saturn Flyby
Figure 7: STK Animation of the Saturn Flyby
Neptune Flyby
The next situation analyzed was a Neptune flyby. The same initial conditions were kept, and a similar analysis was done. Using the velocity of New Horizons after its Jupiter flyby, a trajectory was created to Neptune, here, the velocity was changed to that needed for a Hohmann transfer from Neptune to Pluto. Once again, this maneuver will take a significantly longer amount of time as the semi-major axis of the ellipse created is the the largest as seen from Figure ().
The plot on the right again shows the spacecrafts heliocentric velocity with respect to its distance from the sun. Once again, the Jupiter gravity assist can be seen, as well as the gravity assist around Neptune. The spacecraft leaves Jupiter with a velocity of 21 km/s and approaches Neptune with a heliocentric velocity of 12.6 km/s, resulting in an excess velocity of 7.17 km/s. The heliocentric velocity the spacecraft leaves Neptune with is 5.78 km/s, departing on a Hohmann transfer to Pluto. The maneuver reduces the speed of the spacecraft by 6.83 km/s. The radius needed for the flyby is 108050 km from the center of Neptune and results in the spacecraft being turned 127.27 degrees after a leading side flyby. The spacecraft now arrives at Pluto with a heliocentric velocity of 4.40 km/s, resulting in an excess velocity of 0.33 km/s. The needed Delta V to orbit is reduced to 0.23 km/s. This is a major decrease from the Delta V New Horizons needed to orbit. This comes at the major expense of time. The total transfer time from Earth to Pluto now becomes 109.59 years. This is far to long for any mission to be expected to survive.

Figure 8: Speed through the solar system with a Neptune flyby
While this simulation proved the transfer time is immense, it helped provide some insight into how an orbiter about Pluto could come into play. Gravity assists from external planets could prove to be incredibly useful, as they decrease the velocity of the spacecraft without the use of any fuel. The limiting factor in the transfer time is the transfer orbit from the planet which the gravity assist is performed about and Pluto. This value needs to be small to decrease transfer time, but large to decrease the needed Delta V on arrival. Another conclusion that could be made is to do the gravity assist breaking about the furthest planet away as possible. This allows the spacecraft to keep its large velocity after the Jupiter assist for as long as possible. If this is done, and the transfer orbit from the outermost planet to Pluto is minimized, the Delta V needed at arrival could also be minimized. A summary of the results can be seen below: